“If you want to find the secrets of the universe, think in terms of energy, frequency, and vibration.” — Nikola Tesla
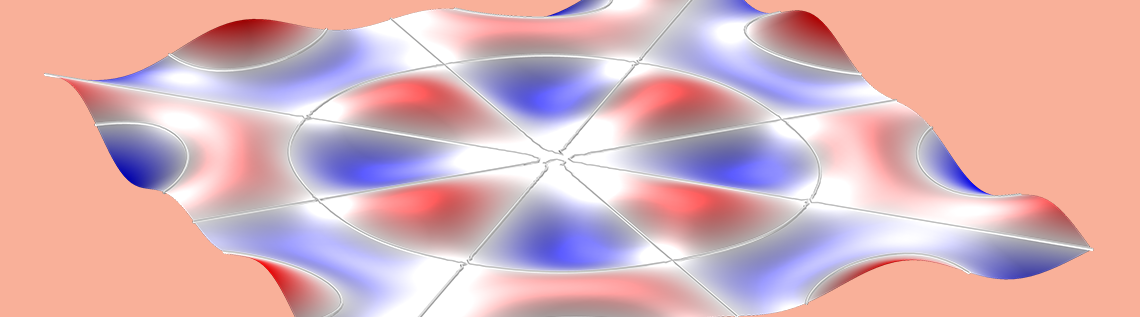
Can we “see” sound? Not directly, but we can come close. By changing our perspective, we can learn a lot about the nature of acoustics. One way to observe acoustics phenomena is by studying standing waves in a solid medium known as a Chladni plate. A special technique creates patterns on the plate that reveal sound’s physical nature.
Visualizing the Resonance of Musical Instruments
Imagine you’re at a classical music concert. The orchestra has finished warming up. The lights dim. A single spotlight appears on the violin soloist as she moves front and center stage. She raises her bow and a hush falls over the audience as you anticipate her first, resounding note. The violinist draws the bow across the string…and the note that results carries beautifully, reverberating throughout the auditorium for your listening pleasure.

Musicians warming up on stage before performing. Image by Jiaqian AirplaneFan — Own work. Licensed under CC-BY 3.0, via Wikimedia Commons.
Aside from the violinist’s talent and training, the quality of the violin plays a large role in the sound produced. Musicians are very particular about their instruments, and rightly so, because an instrument’s design affects its resonance. For instance, when bowing a string, the string vibrates at a certain frequency, which is measured by how many times per second it oscillates back and forth. It’s critical that the bridge and body of a violin are optimized to transmit the energy of that vibration — otherwise, the resonance will be minimal.
Violins and other string instruments are designed and constructed by testing the optimal position of the holes, thickness of the wood, and placement of internal rebars, among other factors. It’s also possible to visualize the geometry of the different types of vibration, called Chladni patterns, that are possible in a violin via a Chladni plate.

A photograph of a violin-shaped aluminum Chladni plate showing a Chladni pattern. Image by Stephen Morris — Own work. Licensed under CC BY 2.0, via Flickr.
How do Chladni plates work and how did they come about?
Ernst Chladni: Exploring Meteors and Music
We now know that sound propagates in waves through a solid, gas, or liquid medium — but we didn’t always know this. In the late 1700s, a German scientist named Ernst Chladni was the first to show that sound travels via waves by devising a way to visualize their vibrations.
Shortly after obtaining a law degree, Ernst Chladni made an abrupt career change that led him to become known as both the “father of meteoritics” and the “father of acoustics”. Chladni’s own father was a law professor and disapproved of his son’s interest in science, pressuring him to follow in his footsteps and become a lawyer. Chladni dutifully did what was expected of him, but shortly after graduating from law school in 1782, he received news of his father’s death. While this must have been a difficult time for Chladni, he felt free to pursue the career he actually wanted and turned his attention to physics.
Ironically, Chladni’s legal background gave him an advantage in this science: Having gained experience in reviewing eyewitness testimony for court cases, he used similar methods to support his theory that meteors are extraterrestrial rather than volcanic in origin, which was the prevailing consensus at the time.
Chladni researched all he could about objects falling from the sky and found people who witnessed the events and had heard and seen similar phenomena: masses of rock falling to the ground, fireballs, explosions, and sonic booms. After compiling the most reliable eyewitness reports, Chladni was able to estimate the speeds at which the rocks entered the atmosphere. He concluded that these extremely high speeds, in addition to the rocks’ scorched appearance, were only possible if the rocks came from outer space.
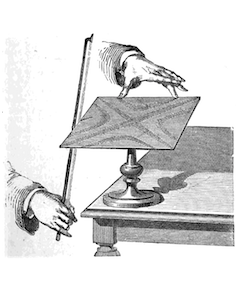
Left: Ernst Chladni. Image in the public domain in the United States, via Wikimedia Commons. Right: Illustration of the Chladni plate technique. Image in the public domain in the United States, via Wikimedia Commons.
Chladni also paved the way for experimental acoustics. It was perhaps the physicist’s interest and ability in music that inspired him to pursue the field, inventing new instruments based on inventions of Benjamin Franklin and Robert Hooke, including the euphone and the clavicylinder. He toured with his instruments across Europe, giving demonstrations and explaining the science behind their designs.
Among his achievements, he was able to determine sound velocities in gases using an organ pipe and developed Chladni’s law. This formula relates the frequency of modes of vibration for a flat circular plate. Among other applications, Chladni’s law can help predict patterns of vibration on flat surfaces and describe the vibration of cymbals and bells.
Chladni’s interest in music and acoustics led him to consider an instrument’s shape and symmetry, fostering the idea for which he is best known…
Finding the Art in Acoustics with Chladni Plates
Inspired not only by Robert Hooke’s instruments but also his experiments with visualizing nodal patterns, Ernst Chladni developed a technique of his own to show modes of vibration on a metal plate.
Here’s How It Works
The shape of a Chladni plate can be square, rectangular, circular, or even shaped like a violin or guitar body, as long as it has a fixed constraint at the center. (In Chladni’s case, he took a flat, rectangular metal sheet and secured it in the center to a sturdy base.) The plate is dusted with a material in order to see the patterns, such as flour, sand, or salt. (We used sand for our experiments!) Next, the plate is excited by drawing a violin bow across the side of the plate until it reaches resonance.
When the plate is excited, some areas vibrate and some areas don’t move. More specifically, you are able to see the standing waves along the nodal lines of the plate. The sand moves away from the antinodes, where the amplitude of the standing wave is maximum, and toward the nodal lines, where the amplitude is minimum, forming patterns known as Chladni figures.
Note: Turn down your sound before playing this video. The note generated by the Chladni plate is quite jarring, and not exactly music to your ears…
Depending on your level of dexterity, you can “play” a Chladni plate by holding the different nodes and exciting it with a bow at different antinodes. The distinct patterns change and vary, depending on the tone.
Many of these patterns are quite interesting:
Two Chladni figure patterns on the same plate in different modes.
We’ve seen how the patterns on a Chladni plate are created, but what do they mean?
All objects, including Chladni plates, have a set of natural frequencies at which they vibrate. A system, such as standing waves in a musical instrument, tends to vibrate at certain discrete frequencies called natural frequencies or eigenfrequencies. Once vibrating at a certain frequency, a structure deforms into a corresponding shape: the eigenmode.
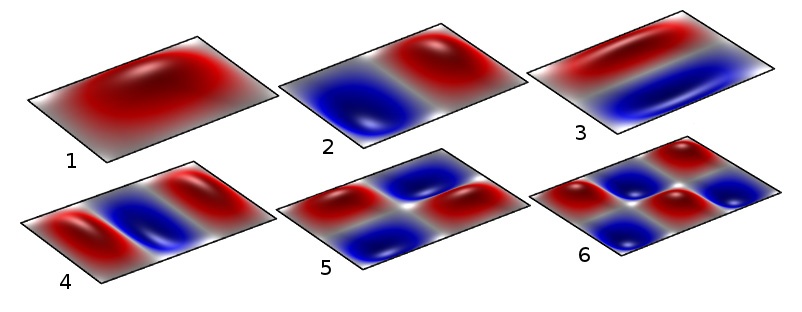
The first six eigenmodes of a simply supported rectangular plate.
A plate is a continuous system that shows eigenfrequencies that depend on geometry, material properties, and constraints. The number of eigenfrequencies it can exhibit is infinite. The modes that are excited enough to make an impact are especially of interest. A plate’s natural frequencies depend a lot on shape and support conditions on the edges of the geometry, as well as its bending stiffness. In instrument production, for example, eigenmode frequencies measured in hertz relate to the stiffness of the wood.
A representation of Chladni patterns on a guitar plate. Compare the left image at a lower frequency (109 Hz) with the right image at a higher frequency (426 Hz).
“Seeing” Sound with Structural Mechanics Simulation
Visualizing sound has applications in many areas, such as furniture placement in a room and analyses of fluid-filled pipes. Visualizing sound can even help building engineers design a concert hall so the acoustics of the building don’t interfere with the violinist’s masterful rendition of Paganini’s Caprice No. 24. By studying sound’s variations, wave forms, wavelengths, speed, and other properties, we can better understand how to manipulate and reproduce sound, as well as account for its physical effects in designs.

An example of a Chladni plate model.
Structural analysis software enables you to simulate the properties of structural vibrations in plates, shells and membranes — with a Chladni plate as a basic example for doing so. The Structural Mechanics Module, an add-on product to the COMSOL Multiphysics® software, includes functionality that makes it easy to set up a plate geometry in a variety of shapes and account for a fixed constraint in the center. You can choose the plate material, usually either steel or aluminum, from the available selection in the Material Library.
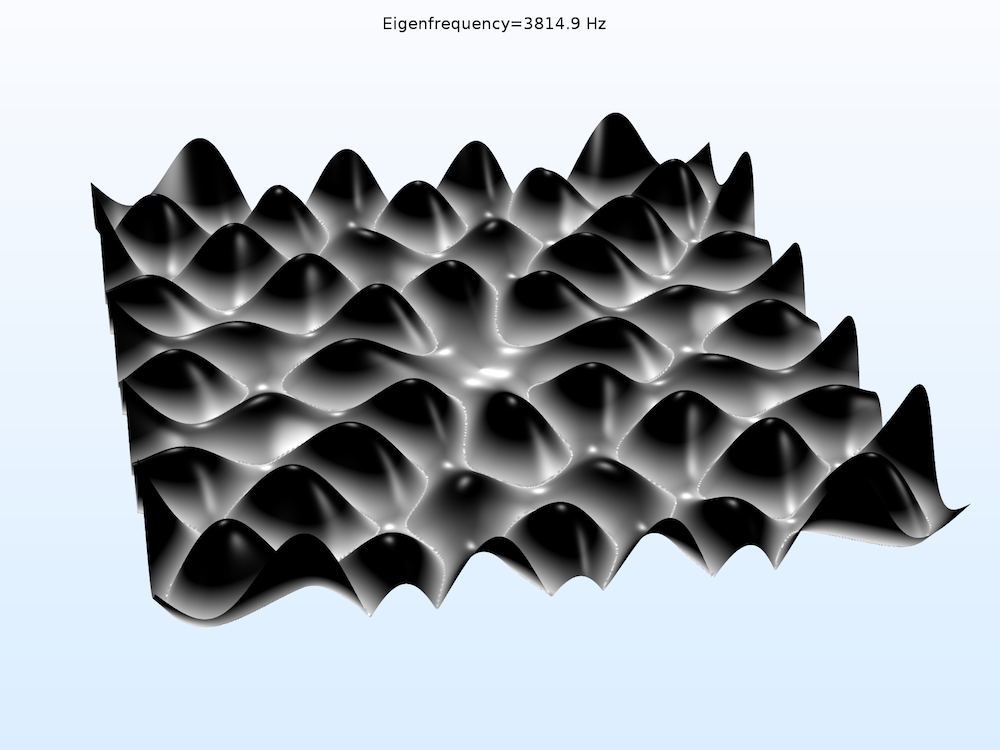
The COMSOL® software also includes predefined physics settings for running an eigenfrequency study. Results from this study show the Chladni figures that form at different frequencies. As shown below, the patterns formed at 610 Hz vary greatly from the patterns formed at 3815 Hz. The analysis of sound waves at the different frequencies of a Chladni plate can be applied to other design projects involving the physical effects of sound.
Chladni simulation at 610 Hz (left) vs. 3815 Hz (right).
Taking the functionality a step further, a COMSOL Multiphysics model of a Chladni plate can be transformed into a specialized user interface called an app. The simulation specialist can build an app with restricted inputs and outputs from the simulation for ease of use. This way, people without simulation expertise still have a way to visualize the Chladni patterns and experiment with the parameter changes, without having to figure out the underlying model.
A screen recording of the Chladni Plate app.
Applications of Chladni Plates Beyond Sound
While many methods of visualizing sound have replaced Chladni’s technique, scientists still see its potential for studying physics phenomena. For instance, physicists tend to agree that the particle motion of nodal lines is random and therefore can’t be controlled — but researchers have shown that the motion of multiple objects could be controlled on a Chladni plate. One research team used a laser light instead of a violin bow to excite a thin, rigid membrane, and observed a similar effect with small vibrating objects. They then visualized the patterns through an array of quantum dots. This discovery could lead to a device that can detect small gravitational anomalies when designing shielding for nuclear materials.
Whether you’re interested in studying sound waves for multiphysics applications or designing a violin worthy of a standing ovation, Chladni plates are a way to observe the effects and distinct vibrational patterns of different frequencies — thus enabling us to “see” sound.
Next Steps
Try visualizing Chladni patterns yourself. We created an app specifically for this blog post and made it available to you in the Application Gallery.
Further Reading
- Check out these blog posts on further musical applications of simulation:
- Read about recent research into Chladni plates:
- P.H. Tuan et al., “Exploring the resonant vibration of thin plates: Reconstruction of Chladni patterns and determination of resonant wave numbers“, The Journal of the Acoustical Society of America, vol. 137, no. 4, pp. 2113–2123, 2015.












Comments (3)
Gabriel Henrique Armando Jorge
December 7, 2019This is just what I was looking for! Great job done here, both text and model simulation.
I want to know if it is possible, with this model, to make a study in a full range of frequencies, instead of only the eigenfrequencies.
Thks a lot!
Brianne Christopher
December 9, 2019Hi Gabriel,
Thank you for your comment. Your question has been answered in this post on our Discussion Forum: https://www.comsol.com/forum/thread/247892/chladni-plate-simulation-app-how-to-change-it-to-visualize-a-continuous-range-of
Please reach out to support@comsol.com if you have any additional questions about your modeling problem.
Best,
Brianne
korea student
November 21, 2021I’m a Korean student. I’m going to use your program to present the Chladni pattern. How can I open the MPH file?