
Vacuum technology has many important applications, from semiconductor device and MEMS fabrication, to vacuum coatings for corrosion protection, optical films, and metallization. The new Molecular Flow Module provides vacuum engineers with previously unavailable tools for modeling gas flows within vacuum systems.
Free Molecular Flow Limit
Conventional fluid dynamics simulations model the effect of collisions between the gas molecules in a continuum flow by means of a scalar material parameter: the viscosity. Once the mean free path of the molecules becomes comparable to the size of the system, the concept of viscosity becomes less appropriate for describing the gas. This is because collisions with the walls begin to occur more frequently than collisions with other molecules. Eventually, the gas molecules collide only with the walls of the system, in what is known as the free molecular flow limit.
| Flow Type | Knudsen Number |
| Continuum flow | Kn<0.01 |
| Slip flow | 0.01<Kn<0.1 |
| Transitional flow | 0.1<Kn<10 |
| Free molecular flow | Kn>10 |
The transition from continuum flow to molecular flow is described by a dimensionless parameter called the Knudsen number (Kn) that represents the mean free path of the gas molecules divided by a typical length scale of the flow geometry. See our previous blog entry “What is molecular flow?” for more details. As the Knudsen number is increased, different techniques are required for modeling the gas. For continuum flows and slip flows, the Navier Stokes equations for describing fluid motion can be used, with special boundary conditions required for slip flow. Transitional flows and free molecular flows require dedicated tools that take the kinetic effects occurring in the gas into account. The Molecular Flow Module provides interfaces designed to model such flows, which cannot be addressed by conventional CFD software. The transitional flow interface can be used for modeling transitional flows using the discrete velocity method. The Molecular Flow interface solves the flow using the Angular Coefficient Method, described in the next section, and includes a range of advanced features for modeling flows inside vacuum systems at low pressures.
The Angular Coefficient Method
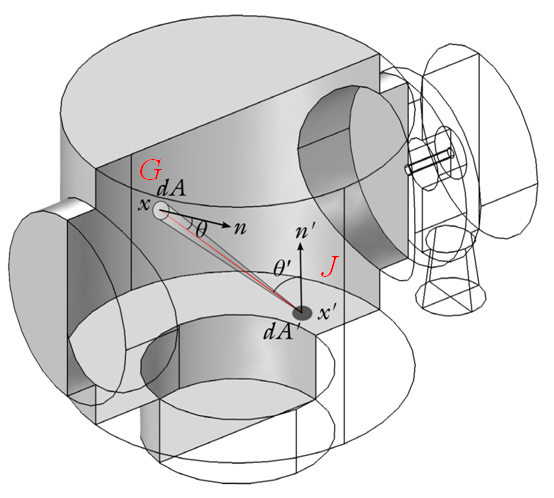
Flux of molecules computed by the Molecular Flow interface.
The Molecular Flow interface computes flux of molecules arriving at a point x (shown in the figure above) on the surface by means of the angular coefficient method. For each point x’, with an associated area element dA’, a certain fraction of the emitted flux reaches x. By integrating over all points x’, the method can compute the total flux arriving at x. Additional integrals are required to compute other parameters, such as the number density, pressure, and heat flux (all of which can be computed by the Molecular Flow interface). Boundary conditions for the method consist of relationships between the outgoing flux (J) and the incoming flux (G). For example, for a simple reflective wall, J=G, while for the surface of a pump, J<G. The method requires that the molecules emitted from a surface have a velocity and angular distribution independent of the direction and velocity of incidence. This assumption, known as total accommodation, is often good for vacuum systems, which typically have rough surfaces. The figure below shows typical trajectories of several gas molecules through a system:

Gas molecule trajectories.
The Molecular Flow Module
Advanced simulations of gas flow through vacuum systems are possible with the Molecular Flow Module. With this module you can easily set up and optimize vacuum systems using a range of boundary conditions that capture effects such as outgassing, pumping, and molecular effusion from an adjacent reservoir. Chamber pump down can be simulated using features for tracking the adsorption and desorption of gas molecules on the walls of the system as a function of time. If you need to evaluate the number density along a beam line through the center of the geometry, the Molecular Flow Module has this functionality, although the equations for the flow are solved only on the surface. Features for evaporation and deposition can be used to study thermal evaporation in a vacuum system. Non-isothermal flows are fully supported and multiphysics simulations coupled with the heat transfer equations are possible. It is also possible to model the flow of several species through a system including interactions between the species that occur on the walls of the chamber. You can even use equation-based modeling to describe complex effects in an efficient manner — for example, the Differential Pumping example explains how to couple a transitional flow through a narrow tube to a molecular flow model, using analytic expressions to capture the flow rate through the tube. An example simulation, which tracks the migration of water introduced into a system through a load lock, is shown in screenshot below.
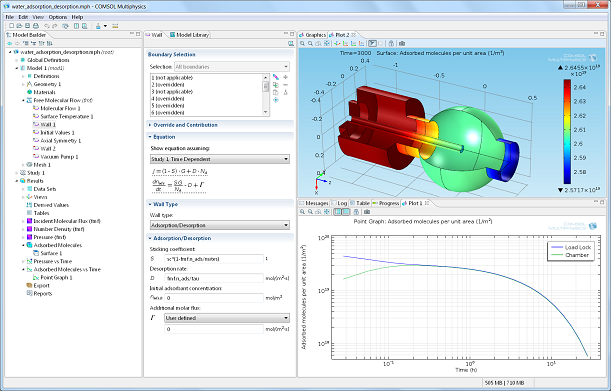
Simulation of the migration of water molecules through a vacuum system. The water is introduced into the system when a gate valve separating the main chamber (right) from a load lock (left) is opened.





Comments (0)