Problem Description
Transient models involve computing a solution that varies over time. To do so, the software begins with the given initial conditions and computes the evolution of the unknowns using one of several different time-integration schemes. Sometimes, these will converge slowly, or not all. This article provides guidance in how to address such cases.
Solution
Background
The COMSOL Multiphysics Time Dependent (transient) solvers have the capability of solving a set of equations of the form:
where
and
can be constants or nonlinear functions of
and
. These equations may be a set of independent ordinary differential equations (ODEs) or a set of coupled equations which arise as a consequence of the spatial discretization of a boundary value problem (BVP) via the finite element method (FEM). Most problems in COMSOL wherein you solve for the time- and spatially-varying fields fall into the latter category. In combination with the above equation, the software can consider a set of algebraic equations of the general form:
and these two sets of equations form a differential-algebraic system of equations (DAE). It is this DAE, along with a set of initial conditions,
, that completely defines a transient model. Note also that models with higher time-derivatives can be addressed, and would simply require introducing additional intermediate variables.
Time stepping methods
There are three classes of methods available within COMSOL for solving DAEs: the BDF, Generalized alpha, and Runge-Kutta Methods. BDF and Generalized alpha are implicit methods while the Runge-Kutta methods are explicit. Explicit methods directly compute the solution at future states based upon the solution at the current state. Implicit methods form and solve a system of equations in terms of the solution at the future state and current state. Implicit methods are generally more stable and faster than explicit methods, but explicit methods will use less memory. The software will automatically determine the most appropriate method based upon the physics interfaces used, it is very rarely recommended to override the default solver method.
To see which of these solvers is being used, look at the Time Stepping settings of the Time-Dependent Solver node within the Solver Configurations, as shown in the screenshot below.
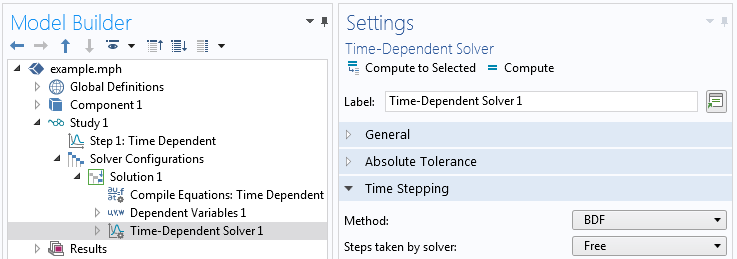
Where to see which solver method is being used.
The Runge-Kutta methods are used primarily for solving systems of ODEs and for models involving the Time Explicit Pressure Acoustics and Time Explicit Electromagnetic Waves physics interfaces. As such, they are quite narrow in their usage, and are not covered within the scope of this Knowledgebase Article.
The Generalized alpha method is generally the default for models where the solution is known to be oscillatory (wave-like) in nature, such as acoustics, wave electromagnetics, and structural transient models that consider inertial terms. These types of problems are best solved by specifying the element sizes and the solver time step. See the article on Resolving time-dependent waves for guidance in how to set up the mesh and choose the time step size and also see KB 1244: Solving Wave-Type Problems with Step Changes in the Loads. Following these guidelines should resolve most convergence issues for this class of models.
The BDF method is generally the default for FEM models involving diffusion, convection, and reactions and such cases represent the majority of cases that benefit from tuning of solver settings. These cases are solved using an adaptive, or Free time stepping scheme where the solver will adjust the time step size automatically. It is these cases that are the focus of this Knowledgebase Article.
It is important to note that, by default, the solvers return the solution at the requested time steps, not the time steps actually taken by the solver. For more details on this, and to see how to override this behavior, see Knowledgebase 1254: Controlling the Time Dependent solver time steps.
Tuning of the time-dependent solver
For problems involving diffusion, convection, and reactions which are by default solved using the BDF method with free time stepping, it is important to be aware of all of the following points. All of these, in combination with each other, will affect solver convergence.
Using Events for Modeling Step Changes
If the loads or boundary conditions on a model are going to be changing instantaneously in time (either at known times, or under known conditions) such cases should be addressed by introducing an Events interface. See: Solving Models with Pulsed Loads in Time. Events ensure that the solver will accurately capture all step changes in loads.
Solver Relative Tolerance
When using adaptive time stepping (with any solver method) the software automatically adjusts the size of the time step taken such that the desired relative tolerance is satisfied. Although the exact choice of time step size in this case is quite complicated and not directly controllable, what is controllable is the Relative Tolerance as shown in the screenshot below. You should always perform a tolerance refinement study: re-solving the model with tighter tolerance and comparing results.
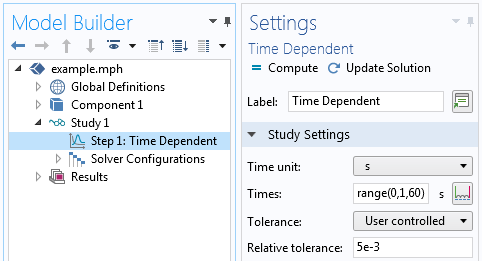
The user controlled relative tolerance setting.
Relative tolerance is related to both the instantaneous error and accumulated error over time. Since errors can accumulate and grow in magnitude, a too-loose relative tolerance can lead to a solution that is error dominated. If you observe the solver initially taking relatively large, and then later on taking relatively small, time steps this can be a cause. Re-solving with a tighter relative tolerance will lead the solver to take smaller time steps initially, but there will be less accumulated error, so the solver may not need to reduce the time step to overcome accumulated errors at later time steps. That is, a tighter relative tolerance can lead to faster overall convergence.
Mesh
The mesh must be sufficiently fine enough to resolve variations in the solution fields over the modeling domains. Especially for problems involving diffusion, convection, and reactions it is not possible to say ahead of time where the spatial variations in the fields will be significant. If the mesh is too coarse then the solver may need to take very small time steps to keep the error down. Therefore, refining the mesh can result in the solver taking larger time steps albeit at the cost of a larger model. Always perform a mesh refinement study as described in Knowledgebase 1261: Performing a Mesh Refinement Study
Mesh refinement and relative tolerance refinement go hand in hand. Study both, alternating back and forth between investigating the relative tolerance and mesh refinement.
Consistent Initialization
You can set up a model with boundary conditions that are inconsistent with the initial values. Such models are still solvable when using Consistent Initialization, which is enabled by default. This, however, may not produce exactly the desired effect and might lead to very small time steps at the beginning of the simulation. For more details, and guidance in how to address this, see Knowledgebase 1172: Solving time dependent models with inconsistent initial values.
Scaling
For numerical reasons, the software always scales the unknowns being solved for. This happens automatically, and if the scaling is appropriate there will be no issue. However, if the scaling is not appropriate then you will need to manually scale the fields. To learn how to check and manually adjust the scaling of variables, see Knowledgebase 1240: Manually Setting the Scaling of Variables.
Nonlinear Solver Settings
When solving a model with significant nonlinear terms, the solver may not be able to compute the solution to the implicit set of equations using the default settings. To understand how to diagnose and resolve such cases, see Knowledgebase 1127: Improving convergence in nonlinear time dependent models.
Initial Time Step
When the solver starts, it estimates an initial time step size to take based upon the total simulation time. Thus, if you solve the same model twice, for different total times, the initial time step can be different. This can lead to different results if there is something significant happening immediately after the start time. To specify the initial time step size, go to the Time-Dependent Solver settings, Time Stepping section, enable the Initial step: option and enter a fixed initial step size, as shown in the screenshot below. Note that the software is still free to choose a time step smaller than this value, but will not make it larger. Also consider if Events can be used instead.
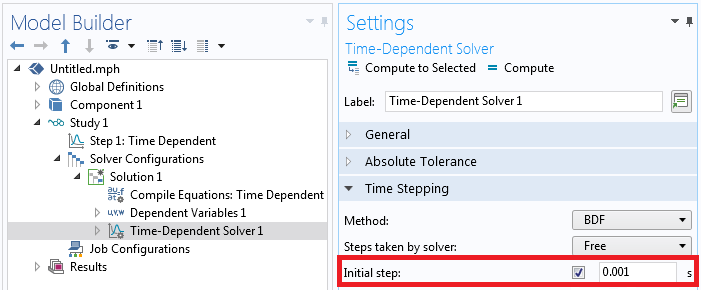 Specifying the initial time step size that the solver tries to take.
Specifying the initial time step size that the solver tries to take.
Segregated vs. Fully Coupled Approach
When solving a multiphysics model, the default behavior of the software is often to treat the problem in a segregated sense, solving for first one physics, then the next, and iterating between all of them at each time step. Depending upon the nature of the problem, this can strongly affect convergence. If the model is being solved with a Segregated approach, try the Fully Coupled, and vice-versa. If solving via the Fully Coupled approach, you will likely need to use a Direct linear system solver. To understand the differences between these approaches and linear system solvers, see: Knowledgebase 1258: Understanding the Fully Coupled vs. Segregated approach and Direct vs. Linear solvers.
Dealing with Non-convergent Models
If the time-dependent solver fails to converge it will either fail immediately, at the initial conditions, or it will fail at some point during the simulation time-span.
If it fails at some point during the simulation, then use all of the techniques described above to improve convergence. In addition, output the results taken by the solver as described in Knowledgebase 1254: Controlling the Time Dependent solver time steps. Plot and observe the solution at, and immediately before, the time step where the solver fails. It can also be helpful to use Probes to monitor a few quantities of interest, as described in Knowledgebase 1255: Reducing the amount of solution data stored in a model. Plotting the results can particularly highlight if the mesh is not fine enough or if there is some accumulated error that is being propagated.
If the solver fails immediately, it is first important to check carefully the initial conditions specified within each physics interface, as well as all of the boundary conditions, loads, and constraints on all physics in the model. If these are inconsistent it can lead to solver failure. The solver will, by default, attempt to correct for this by finding an initial condition that is consistent with all of the boundary conditions, however this may be very different from what is expected. This occurs particularly often for models involving flow, as discussed in Knowledgebase 1172: Solving time dependent models with inconsistent initial values.
If it is reasonable to do so, it is also recommended to try to set up an equivalent, or nearly equivalent, stationary (time-invariant) model as this can serve as a good testbed for investigating mesh refinement, scaling, and comparing segregated versus fully coupled approaches. For information on addressing nonlinear stationary models, see: Knowledgebase 103: Improving Convergence of Nonlinear Stationary Models.
COMSOL makes every reasonable effort to verify the information you view on this page. Resources and documents are provided for your information only, and COMSOL makes no explicit or implied claims to their validity. COMSOL does not assume any legal liability for the accuracy of the data disclosed. Any trademarks referenced in this document are the property of their respective owners. Consult your product manuals for complete trademark details.
